
Элективный курс «Фракталы: геометрия красоты» для 10‑го класса.
Актуальность выбранной темы: фракталы существуют в окружающей нас среде. С помощью фракталов открываются новые возможности в различных областях науки. Их используют в своей работе учёные, инженеры, программисты, дизайнеры.
Так же фрактальные структуры широко встречаются в природе (листья, береговые линии, облака), в техниках (антенны, сжатие изображений), в науке (структура межгалактического пространства, турбулентность). Курс повышает мотивацию к математике через изучение визуально привлекательных и практично значимых объектов.
Цель работы: познакомиться с миром фракталов, научиться их распознавать.
Задачи:
1) Понять, что такое фрактал.
2) Изучить историю их открытия.
3) Рассмотреть некоторые виды фракталов, найти их в окружающей среде.
4) Понять их значимость в мире.
5) Создать собственный фрактал.
Методы:
-сбор информации касаемой темы в интернете, литературе и других источниках;
-анализ и обработка полученной информации;
-проведение исследования;
-создание презентации, иллюстрирующей собранный материал.
Поэт должен видеть то, чего не
видят другие. И это же должен и математик.
— Софья Ковалевская.
Геометрия, которой мы пользуемся в повседневной жизни, восходит к Эвклиду. Треугольники, квадраты, круги, параллелограммы, параллелепипеды, пирамиды, шары, призмы - типичные объекты, рассматриваемые классической геометрией. Предметы, созданные руками человека, обычно включают эти фигуры или их фрагменты. Однако в природе они встречаются не так уж часто. Действительно, похожи ли, например, лесные красавицы ели на какой-либо из перечисленных предметов или их комбинацию? Легко заметить, что в отличие от форм Эвклида природные объекты не обладают гладкостью, их края изломаны, зазубрены, поверхности шероховаты, изъедены трещинами, ходами и отверстиями.
Обычная геометрия не способна описывать форму облака, горы, береговой линии или дерева. Облака — не сферы, горы — не конусы, береговые линии — не окружности, древесная кора не гладка, и молния — далеко не прямая... Природа демонстрирует нам не просто более высокий, а совершенно иной уровень сложности.
Оказывается, почти все природные образования имеют фрактальную структуру. Что это значит? Если посмотреть на фрактальный объект в целом, затем на его часть в увеличенном масштабе, потом на часть этой части и т. п., то нетрудно увидеть, что они выглядят одинаково. Фракталы самоподобны - их форма воспроизводится на различных масштабах.
Так что же такое сам фрактал?
Фрактал — множество, обладающее свойством самоподобия (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей). Слово фрактал образовано от латинского "fractus" (дроблёный, сломанный, разбитый) и в переводе означает состоящий из фрагментов.
Фракталы не похожи на привычные нам фигуры, известные из геометрии, и строятся они по определенным алгоритмам, а эти алгоритмы с помощью компьютера можно изобразить на экране. Вообще, если все слегка упростить, то фракталы – это некое преобразование многократно примененное к исходной фигуре.
Свойства фракталов:
Слово «фрактал» употребляется не только в качестве математического термина. Фракталом может называться предмет, обладающий, по крайней мере, одним из указанных ниже свойств:
1) Обладает нетривиальной структурой на всех масштабах. В этом отличие от регулярных фигур (таких как окружность, эллипс, график гладкой функции): если рассмотреть небольшой фрагмент регулярной фигуры в очень крупном масштабе, то он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, то есть на всех шкалах можно увидеть одинаково сложную картину.
2) Является самоподобным или приближённо самоподобным.
3) Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.
4) Они создаются с помощью простой рекурсивной (повторяющейся) процедуры.
- Учитель: Мария Варанович

Цель: Проследить историческое развитие фундаментальных математических концепций и понять их взаимосвязь.
- Учитель: Наталья Кустарева
- Учитель: Алексей Щевелев


Геометрическая линия является одной из центральных линий курса математики. Она
предполагает систематическое изучение свойств геометрических фигур на плоскости,
формирование пространственных представлений, развитие логического мышления и
подготовку, необходимую для изучения смежных дисциплин (физики, черчения и т. д.).
Многие вопросы курса геометрии в школе изучаются обзорно, в том числе решение
треугольников, применение тригонометрии и подобия при решении практических задач.
Вопросы, связанные с практическим применением подобия, связи элементов треугольников с
тригонометрическими функциями углов, играют немаловажную роль в развитии
математического мышления учащихся, привития интереса к предмету. Многие задачи
описывают ситуации, с которыми учащиеся встречаются в реальной жизни, но на уроках в
основном их успевают решать учащиеся с высоким уровнем подготовки. Важность
практических задач описывающих реальные ситуации, ориентация на выбор профессии,
связанной со знанием геометрических формул и законов, обусловила выбор данного курса для
учащихся 9 классов.
Цель: создание учащимся условий для самореализации и
самоопределения в профессиональном выборе на основе расширения и углубления знаний при
изучении курса «Геометрия вокруг нас».
Задачи курса:
1. расширение и углубление знаний по геометрии, воспитание научного мировоззрения
учащихся;
2. развитие умений применять полученные знания при решении практических задач на
местности;
3. приобщение учащихся к работе с математической литературой;
4. вовлечение учащихся в практическую, проектную деятельность как фактор личностного
развития.
- Учитель: Елена Мельникова

- Учитель: Елизавета Байрамова
- Учитель: Александра Счасная

Элективный курс «Звездная математика» предназначен для обучающихся 9-х классов общеобразовательных школ и ориентирован на формирование глубокого понимания взаимосвязи математики и естественных наук, особенно астрономии. Данный курс направлен на повышение уровня мотивации учащихся к изучению математики посредством знакомства с удивительным миром космоса, включая исторические факты, научные открытия и новейшие достижения.
Цели и задачи курса:
Основной целью курса является:
- развитие познавательного интереса к предмету математики через погружение в увлекательную область астрономии,
- осознание важности математики для познания окружающего мира и прогресса цивилизации,
- формирование умения применять математические методы для решения задач, возникающих в ходе изучения космоса.
Для реализации цели поставлены следующие задачи:
- ознакомить учащихся с основными историческими этапами формирования знаний о космосе и ролью математики в этом процессе;
- научить школьников пользоваться методиками определения расстояния до звёзд, массе звёзд и другим параметрам небесных тел;
- развивать умение самостоятельно анализировать информацию и проводить элементарные расчёты;
- способствовать формированию научного мировоззрения и развитию творческого подхода к исследованию.
Ожидаемые результаты:
По окончании курса учащийся сможет:
- свободно оперировать математическими инструментами для описания
процессов, происходящих в космосе;
- осмысленно воспринимать современную научную литературу и критически оценивать публикуемые в средствах массовой информации сведения;
- применять полученные знания для самостоятельного построения моделей и разработки небольших проектов, связанных с исследованием космоса.
- Учитель: Алина Ахметова
- Учитель: Яна Потеряева
Курс имеет социально-педагогическую направленность, способствуя повышению финансовой грамотности учащихся 9-х классов.
- Учитель: ольга журавлева
- Учитель: Татьяна Якубова
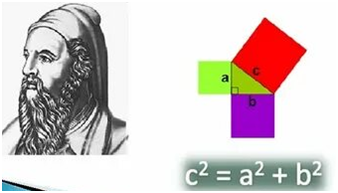
Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с его теоремой. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о "пифагоровых штанах" - квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора это её простота, красота, значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о её широком применении, однако не все знают о нём. Поэтому я заинтересовалась и решила провести исследование.
Объект исследования. Теорема Пифагора.
Гипотеза. Если теорема Пифагора так популярна и сегодня, то в ней заложены такие основы, которые позволяют использовать её в широком диапазоне.
Цели и задачи. Цель работы – показать значение теоремы Пифагора не только в математике, но и других отраслях нашей повседневной жизни.
Исходя из цели, были поставлены следующие задачи:
1. Найти в различных источниках и проанализировать найденную информацию о теореме и биографии Пифагора.
2. Изучить историю появления и развития теоремы Пифагора.
3. Провести опрос среди учащихся в виде анкетирования для выявления знаний о теореме Пифагора.
4. Установить какое значение имеет открытие теоремы в развитии математики.
5. Выяснить где может применяться теорема в повседневной жизни.
6. Обработать полученные данные и сделать вывод.
- Учитель: Татьяна Ковалева
- Учитель: Наталья Трушникова
«Реальная математика» предназначена для учащихся 10 классов общеобразовательных учреждений. Разработана с учетом положения о том, что результатом освоения основной образовательной программы основного общего образования должна стать математическая компетентность учеников, т.е. они должны овладеть специфическими для математики знаниями и видами деятельности, научиться преобразованию знания и его применению в учебных и внеучебных ситуациях, сформировать качества, присущие математическому мышлению, а также овладеть математической терминологией, ключевыми понятиями, методами и приемами.

Общая характеристика учебного предмета.
«Реальная математика» является предметно – ориентированным и предназначен для расширения теоретических и практических знаний учащихся. Он расширяет и углубляет базовую программу по математике, не нарушая ее целостности. Программа проекта содержит задания, в которых ученики совершенствуют навык использования приобретенных знаний и умений в практической деятельности и повседневной жизни, умение строить и исследовать простейшие математические модели. Формулировка этих заданий содержит практический контекст, знакомый учащимся или близкий их жизненному опыту. Такие задания носят название «прикладные задачи».
Решения прикладных задач – это деятельность, сложная для учащихся. Сложность ее определяется, прежде всего, комплексным характером работы: нужно ввести переменную и суметь перевести условие на математический язык; соотнести полученный результат с условием задачи и, если нужно, найти значения еще каких – то величин. Каждый из этих этапов – самостоятельная и часто, труднодостижимая для учащихся задача.
Предлагаемый курс имеет прикладное и общеобразовательное значение: он способствует развитию логического мышления, сообразительности и наблюдательности, творческих способностей, интереса к предмету, данной теме и, что особенно важно, формированию умения решать практические задачи в различных сферах деятельности человека. Решение таких задач способствует приобретению опыта работы с заданием, формированию более высокой, по сравнению с обязательным уровнем сложности, математической культуры учащихся.
Прикладные задачи приучают учащихся пользоваться справочным материалом, заставляют глубже изучать теоретический материал, превращают знания в необходимый элемент практической деятельности, а это важный компонент мотивации учения. Выполняя такие задания, учащиеся оказываются в одной из жизненных ситуаций и учатся отвечать на возникающие вопросы с помощью знаний, полученных на уроках математики.
Программа ориентирована на приобретение определенного опыта решения прикладных задач. Изучение данного курса тесно связано с такими дисциплинами, как алгебра и геометрия. Данный курс представляется особенно актуальным и современным, так как расширяет и систематизирует знания учащихся, готовит их к более осмысленному пониманию теоретических сведений.
- Учитель: Евгения Курманова
- Учитель: Георгий Обзелянский